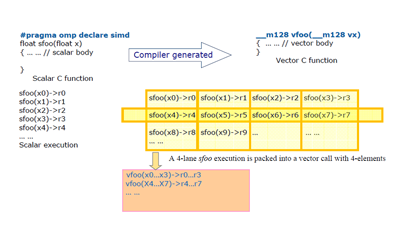
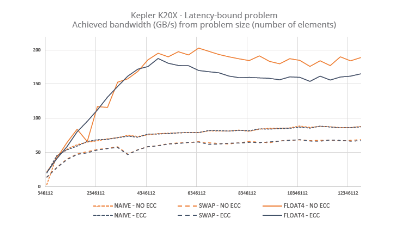
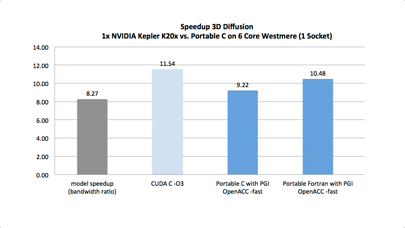
II. ALGORITHMS

The word algorithm can cover different types of problems depending upon the audience. Computer scientists will think in terms of basic programming techniques as explained by Aho et al. [4]. Other scientists in need of high performance computing will likely think more in terms of numerical analysis as introduced by Atkinson [5]. In either cases, the idea is to achieve the desired results with minimal complexity, that is, with a minimal increase in work when augmenting the problem size. Complexity is usually taught in most computer science courses, and numerous books have been written on the subject such as Arora et al [6].

It is usually quite difficult for a computer scientist to replace a numerical algorithm chosen to solve a particular problem by a “better” one. This requires understanding what the code is trying to achieve in computer terms but also in physical (or chemical, astronomical…) terms as well. It also entails understanding the numerical stability, approximation, the boundary conditions, and whatever other requirements might exist for solving the underlying problem. This is something that must be done with involvement someone from the scientific field. More often than not, the constraints of numerical algorithms are such that they unfortunately cannot be changed.

What remains to be studied is the implementation of such algorithms, which quite often are built on top of other algorithms – those of the computer science variety. Matrix inversion, matrix multiplication, finding a maximum value, fast Fourier transforms and so on are the building blocks of many numerical algorithms. They are quite amenable to improvements, substitution and well-studied optimizations.

One of the primary tasks of the optimizer in a numerical code will be to identify these types of conventional algorithms, and make sure the implementation used is the best one for the code. This is usually not a lot of work, as vendor-supplied libraries will include most of them. For instance, the Intel MKL library (accessible in the recent Intel compiler by simply calling the -mkl option to the compiler and the linker) includes full implementations of BLAS or LAPACK [7], fast Fourier transforms including a FFTW3 [8] compatible interface, and so on. One important aspect when using such libraries are their domain of efficiency: extremely small problem sizes are not well suited to the overhead of a specialized library. For instance, large matrix multiplications should make use of an optimized function such as dgemm. Small constant size matrix multiplications (such as 3×3 matrices used in Euclidean space rotation) should be kept as small hand-written functions, potentially amenable to aggressive inlining. In a similar way, whereas large FFT can take advantage of FFTW3 itself or its MKL counterpart, small FFT of a given size can sometimes be readily implemented with the FFTW codelet generator described in [9]. A more work-intensive optimization is the specialization of algorithms for constant input data. For instance, if the small 3×3 matrix mentioned earlier is a rotation around the main axis of a 3D space, the presence of zeroes and one in the matrix can be hard-coded in the function, removing multiple useless operations.

III. PARALLEL CODES

Parallelization is one of the richest and most complex subjects of computer science, and is out of the scope of this paper. Many introductory books have been written on the subject among which for instance [10] [11] [12] [13]. This section deals with running parallel code on contemporary machines without falling into common pitfalls.

III.A – NUMA – All recent multi-socket x86 64 systems are NUMA (Non-Uniform Memory Access), i.e. the latency of a load instruction depends on the address accessed by the load. The common implementation in all AMD Opterons and all Intel Xeons since the 55xx (i.e. Nehalem-EP family) is to have one or more memory controller(s) in each socket, and to connect each socket via a cache coherent dedicated network. In AMD systems the links are HyperTransport, while for Xeons they are QPI (QuickPath Interconnect). Whenever a CPU must access a memory address located in a memory chip connected to another socket, the request and result have to go through the network, adding additional latencies. Such access is therefore slower than accessing a memory address located in a locally connected memory chip. This effect is illustrated in figure 1, which plots the average latency of memory access when stepping through an array of varying size on a dual socket Xeon X5680 Westmere-EP. The first three horizontal plateaus are measurements where the array fits in one of the three levels of caches, while the much higher levels at over 12 MiB measure the time to access the main memory. The four lines represent the four possible relations between the computation and the memory: 0/0 and 1/1 represent access to locally attached memory, while 0/1 and 1/0 represent access to the other socket’s memory. Going from about 65 ns to about 106 ns represents an approximately 63% increase in latency when accessing remote memory.

III.B – NUMA on Linux – To avoid these kinds of performance issues, it is important to understand how memory is allocated (virtually and physically) by the operating system, to ensure memory pages (the concept of paging is among those covered by Tanenbaum [14]) are physically located close to the CPU that will use them. The Linux page size will be 4 KiB or 2 MiB; the last one is more efficient for TLB but is not yet perfectly supported. This page size will be the granularity at which the memory can be placed in the available physical memories.

In Linux, this placement is made by specifying in which “NUMA node” the physical page should reside. The default behavior is only partially satisfactory. At the time the code requires allocation of memory, virtual space is reserved but no physical page is allocated. The first time an address inside the page is written, the page will be allocated on the same NUMA node that generated the write (if that memory is full, the system will fall back to allocating on other nodes). This is a very important aspect. If for one reason or another the memory is “touched” (written to) by only one thread, then all physical pages will live in the NUMA node where the thread was executing at the time. Of course, if the advice from first part was followed, then the thread has been properly “pinned” on the CPU and will not move. This means than any subsequent access by this same thread will benefit from the minimal latency. That’s the good aspect of the behavior.

[4] A. V. Aho and J. E. Hopcroft, The Design and Analysis of Computer Algorithms, 1st ed. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 1974.

[5] K. E. Atkinson, An Introduction to Numerical Analysis. New York: Wiley, 1978.

[6] S. Arora and B. Barak, Computational Complexity: A Modern Approach, 1st ed. New York, NY, USA: Cambridge University Press, 2009.

[7] E. Anderson, Z. Bai, J. Dongarra, A. Greenbaum, A. McKenney, J. Du Croz, S. Hammerling, J. Demmel, C. Bischof, and D. Sorensen, Lapack: a portable linear algebra library for high-performance computers, in Proceedings of the 1990 ACM/IEEE conference on Supercomputing, ser. Supercomputing ’90. Los Alamitos, CA, USA: IEEE Computer Society Press, 1990, pp. 2–11.

[8] M. Frigo and S. G. Johnson, The design and implementation of FFTW3, Proceedings of the IEEE, vol. 93, no. 2, pp. 216–231, 2005, special issue on “Program Generation, Optimization, and Platform Adaptation”.

[9] M. Frigo, A fast Fourier transform compiler, in Proc. 1999 ACM SIGPLAN Conf. on Programming Language Design and Implementation, vol. 34, no. 5. ACM, May 1999, pp. 169–180.

[10] M. Herlihy and N. Shavit, The Art of Multiprocessor Programming. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2008.

[11] T. Mattson, B. Sanders, and B. Massingill, Patterns for parallel programming, 1st ed. Addison-Wesley Professional, 2004.

[12] B. Chapman, G. Jost, and R. v. d. Pas, Using OpenMP: Portable Shared Memory Parallel Programming (Scientific and Engineering Computation). The MIT Press, 2007.

[13] W. Gropp, E. Lusk, and A. Skjellum, Using MPI (2nd ed.): portable parallel programming with the message-passing interface. Cambridge, MA, USA: MIT Press, 1999.

[14] A. S. Tanenbaum, Modern operating systems. Englewood Cliffs, N.J.: Prentice Hall, 1992.