Parfois négligée, l’exploitation des différents formats de représentation des nombres flottants est une voie sûre pour l’optimisation des codes. Voyons comment CUDA se conforme à la révision du standard IEE754, et comment tirer le meilleur parti des formats binary16 et binary128.

Pr David Defour
Manuel Martin
Université de Perpignan

Téléchargez l’intégralité des sources de cet article

La grande majorité des codes scientifiques ont besoin de précision et, dans ce domaine, le format binary64 est la norme. Historiquement, les GPU n’étaient pas destinés au calcul HPC et, par voie de conséquence, s’avéraient assez mauvais pour le calcul en double précision. Le support de la double précision n’est apparu qu’à partir des GT200, avec un slowdown de 8 comparativement à la simple précision. Depuis lors, Fermi et Kepler ont permis de réduire cette différence à un facteur 2-3 (cf. tableau 1) .

On constate néanmoins que, même avec de tels facteurs, les méthodes héritées des générations précédentes telles que celles basées sur la mixed précision ont encore la vie belle. Les processeurs graphiques, même s’ils affichent des débits mémoires importants comparativement à un simple CPU, sont en effet beaucoup plus sensibles que les supercalculateurs sur les problèmes memory-bound – un phénomène qui continuera de s’amplifier à mesure que nous nous rapprocherons de l’exascale. Même si l’on peut espérer un jour avoir la parité en nombre de flops entre SP et DP, la simple précision nécessitera toujours moitié moins de trafic mémoire et d’espace dans les caches et dans les registres.

Si les données sont codées sur moitié moins de bit, on a moitié moins d’information. Aussi, pour certains problèmes, le manque de précision peut devenir critique. Il faut cependant noter que, dans certains cas, on peut conserver la même qualité dans le résultat final en utilisant diverses techniques telles que la mixed precision évoquée plus haut (ie. SpMV, QCD, Solver multigrid) ou sensiblement la même qualité avec des techniques de compensation ou d’arithmétique émulée (sommation…). Ce problème de précision étant un sujet en lui-même, il ne sera pas couvert dans cet article.

IEEE-754

Pour bien cerner le problème, un petit rappel d’IEE754 n’est sans doute pas inutile. Ce standard définit en particulier la représentation des données en virgule flottante (nombres normalisés, dénormalisés, infinis, NAN), les modes d’arrondis, le comportement d’un ensemble d’opérations sur ces formats et la gestion des exceptions. La version actuelle date de 2008 (IEEE754-2008). Son format de représentation binaire (cf. tableau 2) est aujourd’hui le plus utilisé et, logiquement, c’est celui que l’on trouve dans CUDA.

Les flottants se composent de trois champs : un pour représenter le signe, un pour l’exposant et un troisième pour la mantisse. Pour les nombres normalisés, le premier bit de la mantisse est toujours à 1 ; de ce fait, on l’omet dans la représentation, ce qui permet d’économiser un bit.

La majorité des processeurs actuels implémentent en matériel le format binary32 (float) ainsi que le binary64 (double). Depuis peu, on voit se développer du support matériel pour le format binary16 (half) dont on retrouve trace dans le langage Cg de Nvidia apparu en 2002. Ce format ayant été conçu pour le stockage et le transfert des données, il est préférable de ne l’utiliser qu’à cette fin.  Enfin, le format binary128 est encore assez peu utilisé. Parmi les outils qui l’implémentent, citons notamment la dernière version de gcc sur un nombre limité de plateformes.

Les formats supportés nativement par CUDA

CUDA supporte nativement les types simple et double précision et leurs dérivés vectoriels (float{2,4}, double{2,4}), ainsi que les types entiers de 8 à 64 bits (char, short, int, long, long int). Mais ce support est limité pour les types binary16 et les opérations sur 8 et 16 bits (les opérations sur des char et short ont un coût identique aux entiers). En effet, dans ces formats, il est uniquement possible de charger et sauvegarder les données depuis et vers la mémoire, ce qui permet de réaliser des économies en bande passante. Une fois en registre, il suffit de les convertir vers des types supérieurs pour effectuer des opérations.

CUDA permet de réaliser des conversions rapides entre les types, soit à l’aide d’instruction intrinsic, soit à l’aide des unités de texturage. Les instructions intrinsic de conversion entre half et float sont :

float __half2float(ushort x);
ushort __float2half_m(float x);

On constate donc que le type half est encodé comme un entier court non signé (ushort), sachant que la conversion est accélérée en hard.

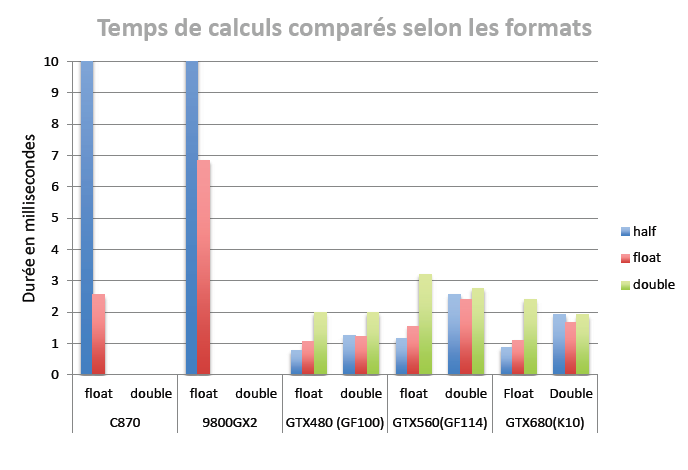
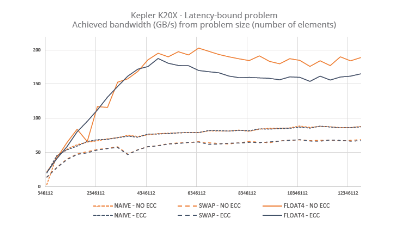
Pour avoir une idée de l’impact de l’utilisation du format half sur les performances, considérons un problème memory-bound comme le problème de la sommation de n nombres appelé aussi réduction. L’idée est de partir du kernel n°6 du programme de réduction présent dans le SDK CUDA et de le modifier pour qu’il accepte en entrée des flottants aux formats binary16, 32 ou 64. Pour  préserver la précision dans les calculs internes, l’accumulateur sera représenté à l’aide d’un float ou d’un double. Le graphique 1 donne les temps d’exécution pour ce kernel. On peut constater que sur ce problème memory-bound, le temps d’exécution est divisé par 2 lorsque l’on passe du format binary64 au format binary32. En revanche, lorsque l’on passe du format binary32 au format binary16 le temps n’est plus divisé que par 1.28.  Nous verrons pourquoi dans les paragraphes suivants.

Voyons maintenant ce qu’il en est de l’utilisation des unités de texturage. Là, le format binary16 est utilisé dans différents environnements graphiques pour stocker des textures avec une plus grande dynamique que ne le permettent les entiers 8 ou 16 bits, et pour un coût inférieur aux flottants binary32. Aussi, dans certains cas, il peut être avantageux de placer les données au format binary16 en mémoire de texture. Accessible en lecture seule, cette mémoire est aussi lente que la mémoire globale mais dispose d’un cache de 8 Ko par multiprocesseur, ce qui autorise des accès rapides en cas de hit dans le cache. Dans les cas où les données manipulées au format binary16 ne sont qu’en lecture seule sur un kernel, et les accès aléatoires, alors il peut être intéressant de considérer cette alternative. 

Le chargement des entiers 8 ou 16 bits à l’aide de l’unité de texturage s’effectue comme ceci :

// Déclaration sur le GPU
texture MaTexture;

// Utilisation dans le Kernel
short2 x = tex1Dfetch(MaTexture, index);

Il est également possible de convertir ces nombres en flottants compris entre 0 et 1 sans surcoût :

// Déclaration sur le GPU
texture MaTexture;

// Utilisation dans le Kernel
float2 x = tex1Dfetch(MaTexture, index);

L’aspect read-only est souvent une contrainte forte mais, avec les binary16, les choses sont légèrement différentes. On a vu que ce format est principalement utilisé pour minimiser les transferts mémoires. Or, dans ce cas, rien n’interdit d’alterner les entrées/sorties en zone de mémoire globale et en zone de texturage entre deux appels de kernels (technique du ping-pong).

Point important, manipuler des données au format binary16 sur le GPU nécessite de pouvoir les créer/convertir sur le CPU. Plusieurs solutions permettent ces opérations. Nous vous recommandons notamment :

– La bibliothèque OpenEXR
– La solution de Jeroen van der Zijp (pour le code basé sur de petites tables).

Maintenant, si l’on se restreint aux nombres normalisés, les conversions se réalisent facilement en utilisant le code suivant :

// Conversion de nombres normalisés
#define __half2float(h)   ((h&0x8000)<<16) h="" amp="" 0x7c00="" 0x1c000="" 13="" 0x03ff="" strong="">
#define __float2half(f) ((f>>16)&0x8000)|((((f&0x7f800000)-0x38000000)>>13)&0x7c00)|((f>>13)&0x03ff)

Alignements mémoire

Rappelons que le stockage dans les registres et les calculs sont réalisés au minimum en binary32 et que seuls les transferts s’effectuent en binary16.  Avec ce format, une attention toute particulière doit être portée aux problèmes d’alignement mémoire (memory coalescing), sachant que, sur les GPU, les accès à la mémoire globale se font en général sur 32 ou 128 octets.

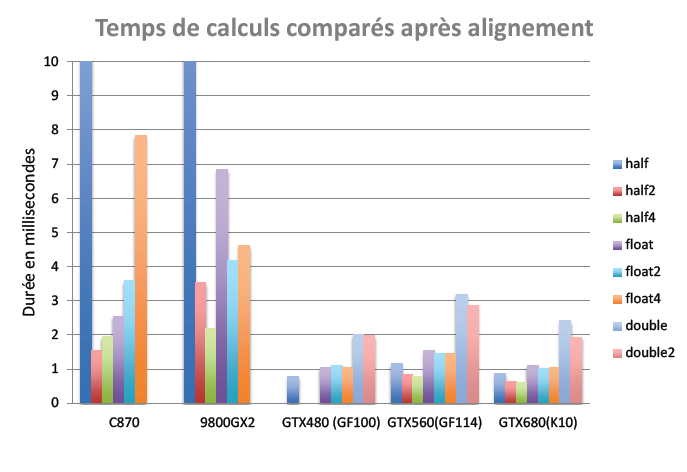
Afin de mesurer l’effet de l’alignement, nous avons ajouté des accès à des types vectoriels dans le code réalisant la réduction de n flottants. Précisons que, contrairement aux architectures AMD, les architectures NVIDIA sont des architectures scalaires. Par conséquent, l’utilisation de types vectoriels n’apporte aucun bénéfice en termes de calcul. Dans le cas considéré, les principaux bénéfices sont liés aux accès mémoires. Le graphique 2 montre les temps obtenus. On constate que l’effet de l’alignement pour le format half est très important sur toutes les architectures  (notamment G80) et permet ainsi d’atteindre un ratio d’environ 1.9 entre le format float et le format half4.

Notez que l’utilisation de ce format ne doit pas être réservée aux transferts entre CPU et GPU ou entre mémoire globale et registres. Il est recommandé de l’utiliser également dans les transferts impliquant la mémoire partagée. En effet, au delà de simplement réduire les transferts, elle permet d’atteindre des facteurs d’accélération supra-linéaire grâce aux effets de cache. Ces effets reposent sur le fait que plus de données peuvent tenir en cache L1, L2, ou en shared memory, ce qui diminue d’autant le nombre d’itérations ou de tuiles à considérer. Ce phénomène n’apparait pas pour le problème de la réduction (la mémoire partagée n’est pas utilisée pour accélérer les accès mémoire). En revanche, pour des problèmes comme la multiplication matrice-vecteur creux et les solveurs PDE ou QCD, il peut se révéler intéressant. Ainsi, dans l’expérience de Clark, Babich, Barros, Brower et Rebbi, l’implémentation d’un solveur QCD basé sur des half était 6.7 fois plus rapide que la version en double et 2.1 fois plus rapide que la version simple.

Il est par ailleurs possible de déclarer des données en mémoire partagée au format half et d’avoir des conversions à la volée, comme ceci :

__shared__ ushort A[SIZE];
float B = __half2float(A[threadIdx.x]);

Cependant, comme pour les accès à la mémoire globale, les accès à la mémoire partagée doivent être bien formés, c’est à dire éviter les conflits de banc.  Avec l’ancienne architecture Fermi, ces accès devaient être réalisé sur 4 octets. Aujourd’hui, avec  Kepler, il est préférable de les coder sur 8 octets. Pour conserver un minimum de backward performance, Kepler permet de sélectionner le mode de placement des données dans les bancs, comme ceci :

// Mode 4 octets
cudaDeviceSetSharedMemConfig(cudaSharedMemBankSizeFourByte);

// Mode 8 octets
cudaDeviceSetSharedMemConfig(cudaSharedMemBankSizeEightByte);

Il est donc conseillé de vectoriser les accès binary16 lors de l’utilisation de la mémoire partagée.

Les formats étendus

Nous avons vu qu’il était possible de gagner en performance en utilisant le format half principalement pour le stockage des nombres et les transferts de données. A l’inverse, il est possible d’augmenter la précision des calculs lorsque celle disponible nativement (binary32, binary64) ne suffit plus.

Pour ce faire, plusieurs solutions sont envisageables. La première repose sur l’utilisation des formats composés (double-double, quad-double). Dans ces formats, un nombre est représenté comme la somme non évaluée de plusieurs nombres flottants.

Une autre solution consiste à utiliser trois champs distincts :  un champ signe, un champ exposant et un champ mantisse, représentés sous la forme d’un vecteur d’entiers. Ce format est beaucoup moins efficace que le premier pour les petites précisions.

Pour certaines fonctions numériques (sommation,  évaluation polynomiale…), il est également possible de considérer les algorithmes compensés. Ils présentent l’avantage d’être rapides mais nécessitent une réécriture du code.

Enfin, si l’on souhaite bénéficier du format binary128, on peut toujours utiliser une version logicielle, par exemple softfloat. Il faut alors ne pas perdre de vue le surcoût engendré par ce type d’implémentation.

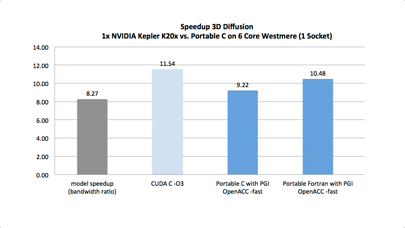
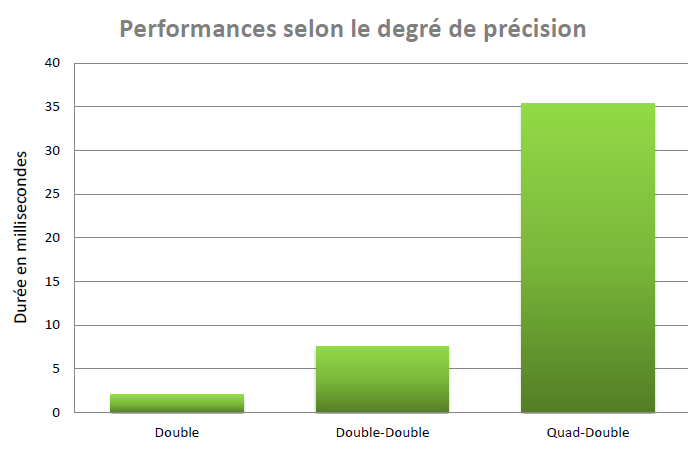
Pour conclure sur le sujet, le graphique 3 nous donne une idée des différences de performances entre les types sur les calculs en grande précision (double : 53 bits, double-double : 107 bits, quad double : 215 bits)

On le voit, l’impact est loin d’être neutre. D’où l’importance de bien évaluer le format avec lequel on travaille. Cette évaluation peut prendre un peu de temps mais, au final, une fois les algorithmes écrits et validés, le gain est loin d’être négligeable.

Bons développements !