La description et la prédiction de processus microscopiques est d’une importance considérable pour l’industrie pharmaceutique, la microélectronique, les nouveaux matériaux, l’industrie du pétrole, etc. À l’échelle des atomes, il est nécessaire d’avoir recours à la mécanique quantique pour décrire correctement le comportement du nuage électronique autour les noyaux.

Résoudre exactement l’équation fondamentale de la mécanique quantique (l’équation de Schrödinger) pour un grand nombre d’électrons est impossible en pratique puisqu’il s’agit d’une équation aux dérivées partielles de dimension 3N, où N est le nombre d’électrons considérés (de quelques dizaines à quelques millions!). Une possibilité est la résolution stochastique de cette équation (cf. HPC Magazine I-6, Septembre 2013), ou bien l’utilisation de méthodes déterministes où la fonction d’onde est exprimée sur une base finie. La méthode déterministe exacte dans la base choisie est l’interaction de configurations complète (Full-CI), avec une complexité de O(N!). Bien entendu, cette méthode ne peut être utilisée que pour quelques électrons. Différents niveaux d’approximation du Full-CI définissent ce qu’on appelle les méthodes post-Hartree-Fock qui ont une complexité entre O(N5) et O(N8).

En 1998, W. Kohn a eu le prix Nobel de Chimie pour la théorie de la fonctionnelle de la densité (DFT). Dans cette approche, la fonction d’onde du système (dans l’espace à 3N dimensions) n’est plus nécessaire pour décrire les propriétés du système. La densité électronique à un corps, qui est une fonction de l’espace à 3 dimensions, suffit. Cependant cette théorie n’est exacte que si l’on connaît la fonctionnelle exacte de la densité, ce qui n’est pas le cas aujourd’hui. Différentes approximations de la fonctionnelle exacte sont utilisées dans les calculs de DFT, et la complexité du calcul est O(N³).

Si l’on veut encore accélérer les calculs, on peut pousser les approximations encore plus loin en utilisant des méthodes dites semi-empiriques. Dans ce cas, les éléments de matrices sont paramétrés soit sur des résultats expérimentaux, soit sur des résultats obtenus avec des méthodes précises sur de petits systèmes. La complexité est toujours O(N³), mais le préfacteur est dix à cent fois plus petit que dans les méthodes DFT car les matrices sont beaucoup plus rapides à calculer.

Si l’on veut étudier la dynamique de systèmes à plusieurs dizaines ou centaines de milliers d’atomes, la complexité cubique n’est pas acceptable. Heureusement, les interactions entre les particules (électrons et noyaux) sont essentiellement locales. Ainsi, il est possible d’obtenir une complexité O(N) pour des systèmes suffisamment grands en introduisant une très petite erreur: Récemment, une équipe de Zurich à réalisé des calculs de 100 000 atomes en DFT et d’un million d’atomes avec une approche semi-empirique (DFTB) sur des milliers de coeurs avec le code CP2K.

Le Challenge

Nous nous sommes placés dans le cadre d’une approche semi-empirique de la DFT (Density Functional Tight Binding, DFTB). Dans le code deMon-Nano, nous avons développé une méthode utilisant la localité des interactions pour rendre le temps de restitution et les besoins en mémoire presque linéaires en fonction de la taille du système. Nous avons choisi une implémentation à mémoire partagée pour plusieurs raisons. D’une part, le calcul des matrices est très rapide, donc la rapport calcul/communications en MPI serait défavorable. De plus, une implémentation MPI utiliserait beaucoup de communications collectives qui sont à éviter. Enfin, les besoins en mémoire sont tels que les systèmes de quelques dizaines de milliers d’atomes peuvent tourner sur des noeuds de calcul standards avec 64 Go de RAM.

Nous avons eu la chance de pouvoir réaliser nos calculs sur la machine SGI Altix UV à 384 coeurs Xeon E7-8837 et 3 To de RAM du mésocentre CALMIP (Toulouse). Cette machine est un agrégat de 24 blades bi-processeurs à 8 coeurs connectés par Numalink, un interconnect propriétaire de chez SGI permettant de connecter directement tous les processeurs entre eux afin de voir cet agrégat de machines comme une machine unique (Single System Image). Ainsi, notre code OpenMP a pu tourner directement sur 376 coeurs de la machine en utilisant plus d’1.5 To de mémoire partagée.

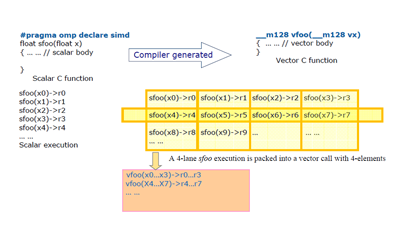
Dans notre algorithme, nous avons réduit le coût de calcul de O(N³) à O(N), et le stockage de O(N²) à O(N). Puisque le nombre d’opérations flottantes est proportionnel au nombre d’accès à la mémoire, notre algorithme est inévitablement memory-bound. Notre implémentation a été optimisée pour les processeurs x86 (vectorisation, équilibrage des additions et multiplications, etc), et les opérations flottantes sont maintenant extrêmement rapides. Il en découle que le goulot d’étranglement est principalement le temps que mettent les données à venir sur le coeur de calcul : la latence moyenne de la mémoire. Sur l’Altix UV, la topologie d’interconnexion des processeurs est telle que les effets NUMA (Non-Uniform Memory Access) sont beaucoup plus forts que sur une machine quadri-socket standard. Voici les latences que nous avons pu mesurer sur l’Altix UV, qui sont caractéristiques d’un processeur Westmere :

     • 1 cycle CPU: 0.37 ns (2.67 GHz)

     • L1: 1.5 ns (4 cycles)

     • L2: 3.7 ns (10 cycles)

     • L3: 16 ns (43 cycles)

Cependant les latences d’accès aléatoire à la mémoire, sont bien supérieures :

     • 195 ns sur le module attaché au CPU qui calcule

     • 228 ns sur le module attaché à l’autre CPU (lien QPI)

     • 570 ns pour l’accès à la mémoire d’une blade voisine (lien Numalink)

     • 670 ns pour l’accès à la mémoire d’une autre blade avec (lien Numalink + 1 saut)

     • 760 ns pour l’accès à la mémoire d’une autre blade avec (lien Numalink + 2 sauts)

     • 875 ns pour l’accès à la mémoire d’une autre blade avec (lien Numalink + 3 sauts)

     • 957 ns pour l’accès à la mémoire d’une autre blade avec (lien Numalink + 4 sauts)

Nous avons mesuré que lors d’accès réguliers à la mémoire, le prefetch hardware fonctionne aussi bien au sein d’une blade qu’entre blades. Ainsi, pour les accès réguliers les communications entre blades peuvent être effectuées de manière asynchrones par le matériel sans intervention du programmeur dans le code source. Compte tenu de ces données, nous avons utilisé les stratégies suivantes pour écrire le programme:

> Réduire la consommation mémoire afin de réduire la probabilité que les données soient sur une autre blade

> Réutiliser le plus possible les données qui sont dans les caches

> Re-calculer certaines quantités à la demande au lieu de les stocker

> Changer les structures de données afin d’avoir le plus possible d’accès réguliers, stride-1 si possible

> Synchroniser les threads le moins souvent possible

> Utiliser un scheduling statique autant que possible, et un scheduling dynamique quand l’équilibrage est vraiment trop mauvais

> Utiliser le plus possible de la mémoire proche. Chaque thread alloue ses tableaux temporaires dans les blocks OpenMP

> Les gros tableaux globaux qui sont toujours accédés dans un scheduling statique sont alloués hors des blocs OpenMP, mais mis à zéro dans une boucle OpenMP statique afin que les pages mémoires soient allouées proche des processeurs qui les utilisent. En effet, la first touch policy ne fonctionne pas pour l’allocation d’un tableau mais pour le premier accès au tableau

> Empêcher la migration des threads lors de l’exécution pour garder la localité des données

Les résultats

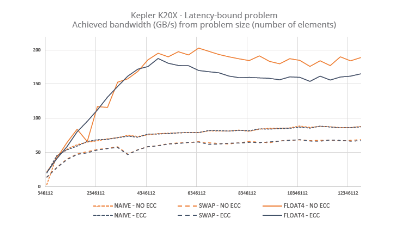
Le benchmark est une boîte cubique, contenant entre 184 et 504 896 molécules d’eau (1.5 millions d’atomes). Les temps de restitution sont donnés sur la Fig. 1.

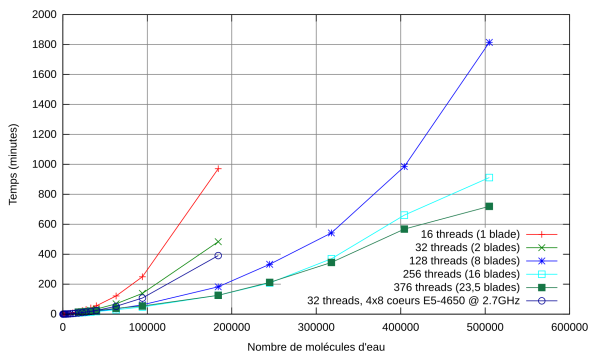
Fig. 1 – Temps de restitution en fonction du nombre de molécules d’eau. Comparaison avec les résultats obtenus sur un serveur Sandy Bridge quadri-socket (32 coeurs, 1 To de RAM).

Nous avons également comparé nos résultats avec ceux obtenus avec l’algorithme usuel en O(N³) qui utilise la routine DSYGV de Lapack. Les erreurs relatives introduites par notre algorithme sont de l’ordre de 10^-12, donc on peut considérer que notre algorithme est presque exact. Pour un système comprenant 2 208 molécules d’eau sur 4 coeurs, DSYGV prend un peu moins de 7 heures, tandis que notre algorithme prend moins de 3 minutes.

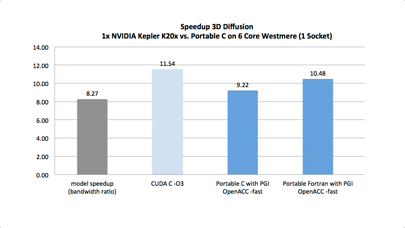
L’algorithme utilisé par l’équipe de Zurich qui a réalisé le premier calcul sur un million d’atomes repose sur l’utilisation d’une bibliothèque MPI pour réaliser des produits de matrices creuses. La comparaison du temps CPU moyen par atome entre CP2K et deMon-Nano est donnée dans la Fig.1. Cette figure montre clairement qu’entre 10 000 et 100 000 atomes, notre code est environ 30 fois plus performant.

Les perspectives

Plutôt que de réaliser un seul calcul sur un système immense, les besoins actuels des chercheurs sont la réalisation d’un grand nombre de calculs sur des systèmes allant du millier à la centaine de millier d’atomes (optimisation de géométrie, calcul de propriétés physico-chimiques par méthodes de Monte Carlo ou dynamique moléculaire, etc.). Nous avons obtenu une efficacité remarquable dans ce régime.

Nous prévoyons d’effectuer une étude en dynamique moléculaire d’un morceau d’ADN dans l’eau (un système d’environ 20 000 atomes), en collaboration avec une équipe du Centre d’Elaboration des Matériaux et d’Etudes Structurales (CEMES). Un tel calcul pouvant tourner de façon très efficace sur un noeud bi-socket avec 64 Go de RAM, nous ajouterons une couche de parallélisme distribué pour le déploiement d’un grand nombre de trajectoires indépendantes.

Les résultats présentés ici ont été réalisés sur une machine exceptionnelle. En effet, peu de laboratoires et de centres de calcul possèdent une machine SMP avec 384 coeurs et 3 To de RAM. Cependant de telles machines seront probablement les noeuds élémentaires d’un supercalculateur dans avenir proche, et ce méso-challenge nous a permis de montrer la robustesse de notre approche.

Anthony Scemama (1), Mathias Rapacioli (1), Nicolas Renon (2)
Université de Toulouse, (1) CNRS – Laboratoire de Chimie et Physique Quantiques, (2) CALMIP.

[Cet article fait partie du dossier Journée Meso-Challenges 2013 : le compte-rendu !]